Life underground
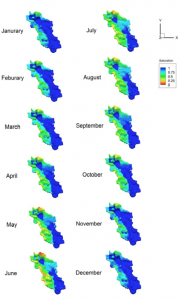
Monthly snapshots of simulated water saturation and distribution at the Disney Wilderness Preservation site in Florida using a unified multiscale model that can describe both groundwater and surface water flow. The blue area is surface water; the other colors denote groundwater at various degrees of saturation. (Pacific Northwest National Laboratory.)
For scientists who develop climate simulations, a major challenge lies directly beneath their feet. Bacteria and archaea – Earth’s prokaryotes, or simple, single-cell organisms – teem in the soil. The top meter of forest soil harbors 40 million prokaryotes per gram. In virtually every other soil type, from deserts to cornfields, that number rockets to 2 billion cells per gram.
And the microbes run deep: Some have been pulled from depths greater than 3,000 meters, says a now-classic 1998 paper from the Proceedings of the National Academy of Sciences. That study notes that the role of these microorganisms in global climate is enormous. Most prokaryotes live in the ocean floor, the soil and the subsurface, 1 to 8 meters below the land and ocean. These microbes may hold as much carbon as all the plants on Earth and certainly contain more than 10 times as much nitrogen and phosphorus.
Because of their content and their roles in photosynthesis and decomposition, prokaryotes govern the sequestration or release of potent greenhouse gases, such as carbon dioxide, methane and nitrous oxide. But many prokaryotes live in a complex habitat of sand, silt, clay and rocks. Their interactions with one another and with their surroundings are complex and ever-changing as water ebbs and flows. As a result, even the most advanced computer models of Earth’s warming climate haven’t captured prokaryotes’ many roles.
But realistically modeling these flows is arduous. For example, a valid simulation would have to describe water as it runs down a creek bed, sinks into clefts and gaps, and seeps into porous beds of sand or massive rock aquifers.
“Soil pore size has a wide range distribution – from nanometers to millimeters – that is over six orders of magnitude difference,” says Chongxuan Liu, a chief scientist at Pacific Northwest National Laboratory (PNNL) in Richland, Washington. “Only large pores in soils – micron scale and up – can be spatially resolved using modern (computing) technologies, and there is a large fraction of soil pores that cannot be resolved. These unresolved soil pores are the mixed media of solids and pores, and are important to understand how water saturates, drains and migrates in soils.” It’s critical that computer modelers develop ways to deal with this mixed media if they’re to realistically simulate water flow through soil, Liu adds.
Such a straightforward, useful modeling approach has eluded scientists until recently – when Liu and his team developed a unified multiscale model that greatly simplified this water-flow problem. Their work was supported by the U.S. Department of Energy’s Office of Biological and Environmental Research through the Terrestrial Ecosystem Science Program. The team’s report on the research was published earlier this year in Soil Science Society of America Journal.
Scientists have long known how to simulate the fluid flow down a channel, in a pipe or even through a mass of material with pores large enough to be measured. For such problems, the Navier-Stokes (N-S) equations are the mathematical toolkit of choice. Invoking classical laws of motion, these equations take friction into account while describing fluid movement.
The limits of Navier-Stokes
However, the N-S equations don’t apply to fluids moving through permeable substances – that is, ones with pores too small to measure. To model water seeping through an aquifer, for example, researchers draw equations based on Darcy’s law. This law relies on factors such as the material’s experimentally determined permeability and the fluid’s viscosity to simulate flows.
But Darcy equations and N-S equations do not dovetail with each other. To simulate the flow of a fluid through a matrix comprised of both types of materials, computer models had to run costly iterative calculations conserving mass and momentum across every boundary between them.
Such simulations are especially difficult because of the enormous challenge of defining all the boundaries between pore regions and porous regions.




