Slippery subject
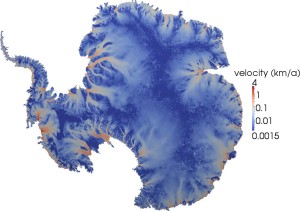These visualizations show ice flow velocity at the surface from satellite observations (top) and as reconstructed from parameters derived by solving the inverse problem. The scale is kilometers per year. The inverse reconstruction most closely matches reality in the critical coastal areas. (Tobin Isaac, University of Texas.)
Climate models are thin on ice. Simulations to predict the impact of climate change are weak in how they portray the flow of polar ice sheets into oceans. Land ice models have been subject to so much uncertainty that in its 2007 Fourth Assessment Report the Intergovernmental Panel on Climate Change said they were too ambiguous to permit reliable predictions of how much ice sheets would contribute to rising sea levels.
Much of the uncertainty arises from input parameters that are difficult, if not impossible, to measure. Researchers can only estimate how much these forces affect ice sheet movement and how much weight to give them in simulations.
One such parameter is basal friction: the resistance to movement at the ice sheet’s base, where it grinds against rocks and earth. “It has a big effect on our predictions,” says Tobin Isaac, a computational and applied mathematics doctoral student at the University of Texas at Austin.
Isaac and other researchers are getting a grip on this unseen parameter. They take observations – satellite measurements of Antarctic ice sheet velocity – and work backward to calculate the basal sliding force that led to them.
Issac and colleagues outline an approach to solve this virtually impossible problem and to calculate the results’ uncertainty in a paper posted online and in a talk Isaac delivered in New Orleans in November at SC14, the supercomputing conference. The method is scalable: The number of steps it takes grows only slightly with the number of variables and parameters it includes.
Among computational scientists, “having the parameters and simulating so you can compare results to observations is called the forward problem,” says Isaac, an alumnus of the Department of Energy Computational Science Graduate Fellowship (DOE CSGF). “Taking the observations and getting back at the parameters you need is the inverse problem.”
However, unseen parameters inferred from observations are bound to be somewhat uncertain. To make model predictions useful, researchers must account for that ambiguity in a process called uncertainty quantification (UQ). With UQ, “we can come to people and say ‘Our best models say this will happen, but this is the part of our prediction we’re most certain about and this is the part we’re less certain about.’”
Models cast a mesh of data points through the space they’re simulating, such as an ice sheet. Algorithms calculate the physical processes at each point. Taken together, they produce a picture, much like pixels produce a digital image. The closer the points are spaced, the more accurate the model is but the more computing it requires.
But “when you ask for a parameter field, you’re not asking for just one or two values,” Isaac says. “You’re asking for one or two values for this section of the ice sheet, one or two values for that section of the ice sheet. Depending on how big you make those sections, you could end up with a very large parameter set” – and an even larger problem. Each parameter adds a dimension to the space of choices algorithms must explore to find values that reproduce the observed data.
