Forceful thinking
Until recently, the Casimir force was a curiosity – a quantum electromagnetic field effect engineers could largely ignore as they went about designing machines and electronics.
The force is getting harder to discount, however, with the rise of microelectromechanical systems, or MEMS – devices like pumps and switches that are thinner than hairs and invisible to the naked eye. When such tiny parts are microns or nanometers apart, the phenomenon Dutch physicist Hendrik Casimir predicted can push them together.
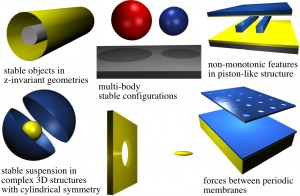
Using mathematical methods he helped develop, Alejandro Rodriguez has calculated Casimir forces in these and other complex structures.
“These objects, because of the Casimir force, tend to stick together and they cease to function,” says Alejandro Rodriguez, a Department of Energy Computational Science Graduate Fellowship recipient who just received a Ph.D. in condensed matter theory at the Massachusetts Institute of Technology. He’s part of a group that is developing new ways to calculate the Casimir force, opening a path to potentially cancel – or harness – it.
In a paper published in May in Proceedings of the National Academies of Sciences, Rodriguez, fellow graduate student Alexander McCauley and professors John Joannopoulos and Steven Johnson describe the theoretical ingredients of a Casimir analog computer. The computer could make it easier to calculate the force.
“Five years ago you could count the geometries for which you could calculate the Casimir forces on one hand,” says Johnson, Rodriguez’s MIT advisor. That’s changed since the four researchers developed algorithms that for the first time efficiently and accurately compute the Casimir force between objects with complex forms. Now if they wanted to, they could “calculate some crazy shape or some complicated periodic structure.”
Johnson says he had a crude proof of concept he developed as a postdoctoral researcher but that Rodriguez “actually turned it into a practical method.”
Tracking in time
Calculating the Casimir force relies heavily, Rodriguez says, on the ability to calculate the Maxwell Green’s function, which characterizes electromagnetic response to electronic sources around the surface of an object of interest. One of several methods he, McCauley, Joannopoulos and Johnson developed is based on the finite-difference time-domain, or FDTD, scheme. As the name implies, the method calculates equations for electric and magnetic fields as they evolve in time, independent of the frequency of electromagnetic conduction.
The method discretizes the partial differential equations used to calculate the Maxwell Green’s function at data points around the complex bodies the researchers want to model. The equations are solved in successive time steps as the electric and magnetic fields respond to current pulses at each data point. Totaling the electric field results provides the Casimir force, with accuracy depending on computer power and time available to run the problem.




